László Kozma :: Research
Research interests
Efficient data structures and algorithms and algorithmic adaptivity. Combinatorial structures (permutations, graphs, set systems, posets) and their algorithmic aspects. Algorithmic geometry and learning.Publications
- Faster exponential algorithms for cut problems via geometric data structures
with Junqi Tan, ESA 2025.
[pdf] - Balanced TSP partitioning
with Benjamin Aram Berendsohn, Hwi Kim, EuroCG 2025.
[pdf] - Theoretical Analysis of Byte-Pair Encoding
with Johannes Voderholzer, preprint 2024.
[pdf] - Online sorting and online TSP: randomized, stochastic, and high-dimensional
with Mikkel Abrahamsen, Ioana O. Bercea, Lorenzo Beretta, Jonas Klausen, ESA 2024, HALG 2025.
[pdf] - Non-adaptive Bellman-Ford: Yen's improvement is optimal
with Jialu Hu, preprint 2024.
[pdf] - An optimal randomized algorithm for finding the saddlepoint
with Justin Dallant, Frederik Haagensen, Riko Jacob, Sebastian Wild, ESA 2024.
[pdf] - Finding the saddlepoint faster than sorting
with Justin Dallant, Frederik Haagensen, Riko Jacob, Sebastian Wild, SOSA@SODA 2024.
[pdf] - Optimization with pattern-avoiding input
with Benjamin Aram Berendsohn, Michal Opler, STOC 2024.
[pdf] - Fast approximation of search trees on trees with centroid trees
with Benjamin Aram Berendsohn, Ishay Golinsky, Haim Kaplan, ICALP 2023.
[pdf] - Fixed-point cycles and EFX allocations
with Benjamin Aram Berendsohn, Simona Boyadzhiyska, MFCS 2022.
[pdf] - Splay trees on trees
with Benjamin Aram Berendsohn, SODA 2022.
[pdf] - Analysis of smooth heaps and slim heaps
with Maria Hartmann, Corwin Sinnamon, Robert E. Tarjan, ICALP 2021.
[pdf] [smooth-heap.c] [slim-heap.c] [slides] - Group testing with geometric ranges
with Benjamin Aram Berendsohn, ISIT 2022.
[pdf] [compact-pdf] - Exact exponential algorithms for two poset problems
SWAT 2020.
[pdf] [talk-notes] - Finding and counting permutations via CSPs
with Benjamin Aram Berendsohn, Dániel Marx, IPEC 2019.
(Journal version: Algorithmica, Vol 83(8), 2021, by invitation.)
[pdf] [journal-link] [slides] - Hamiltonicity below Dirac's condition
with Bart Jansen, Jesper Nederlof, WG 2019.
[pdf] [slides] - Time- and space-optimal algorithm for the many-visits TSP
with André Berger, Matthias Mnich, Roland Vincze, SODA 2019.
(Journal version: ACM TALG, Vol 16(3), 2020.)
[pdf] [journal-link] [talk-notes] - Selection from heaps, row-sorted matrices and X + Y
using soft heaps
with Haim Kaplan, Or Zamir, Uri Zwick, SOSA@SODA 2019.
[pdf] [slides -- Uri Zwick] - Improved bounds for multipass pairing heaps and path-balanced binary search trees
with Dani Dorfman, Haim Kaplan, Seth Pettie, Uri Zwick, ESA 2018.
[pdf] - Smooth heaps and a dual view of self-adjusting data structures
with Thatchaphol Saranurak, STOC 2018, HALG 2019.
(Journal version: SICOMP, Vol 49(5), 2020, by invitation.)
[pdf] [slides] [poster -- Thatchaphol] [journal link] [smooth-heap.c] [slim-heap.c] - Multi-finger binary search trees
with Parinya Chalermsook, Mayank Goswami, Kurt Mehlhorn, Thatchaphol Saranurak, ISAAC 2018.
[pdf] [slides] - Pairing heaps: the forward variant
with Dani Dorfman, Haim Kaplan, Uri Zwick, MFCS 2018.
[pdf] [slides] - Maximum Scatter TSP in Doubling Metrics
with Tobias Mömke, SODA 2017.
[pdf] [slides, extra slides] - Binary search trees, rectangles and patterns, PhD thesis, Saarland University, 2016.
[pdf] [slides] - Binary search trees and rectangulations
with Thatchaphol Saranurak, Technical report, 2016.
[pdf] - Hitting Set for hypergraphs of low VC-dimension
with Karl Bringmann, Shay Moran, N.S. Narayanaswamy, ESA 2016.
[pdf] - Pattern-avoiding access in binary search trees
with Parinya Chalermsook, Mayank Goswami, Kurt Mehlhorn, Thatchaphol Saranurak, FOCS 2015, HALG 2016.
[pdf] [slides I -- Thatchaphol] [slides II] - Greedy Is an Almost Optimal Deque
with Parinya Chalermsook, Mayank Goswami, Kurt Mehlhorn, Thatchaphol Saranurak, WADS 2015.
[pdf] [slides -- Thatchaphol] - Self-Adjusting Binary Search Trees: What Makes Them Tick?
with Parinya Chalermsook, Mayank Goswami, Kurt Mehlhorn, Thatchaphol Saranurak, ESA 2015.
[pdf] [slides] - Streaming Algorithms for Partitioning Integer Sequences
with Christian Konrad, Manuscript, 2014.
[pdf] - Shattering, Graph Orientations, and Connectivity
with Shay Moran, Electronic Journal of Combinatorics, Vol 20(3), 2013.
[pdf] [slides] - Privacy by Fake Data: A Geometric Approach
with Victor Alvarez, Erin Chambers, CCCG 2013.
[pdf] - Minimum Average Distance Triangulations
ESA 2012.
[pdf] [slides] [poster] - Binary Principal Component Analysis in the Netflix Collaborative Filtering Task
with Alexander Ilin, Tapani Raiko, MLSP 2009.
[pdf] [slides]
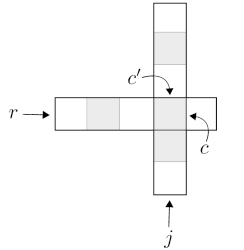
Summary: soon.
Summary: soon.
Summary: soon.
Summary: soon.
Summary: The classical Bellman-Ford algorithm (from the 1950s) solves the single-source shortest paths problem by a sequence of edge-relax operations. It can be implemented in a non-adaptive way, which means that the sequence of edge-relax operations is fixed upfront. Yen's popular variant of the algorithm (from 1970) is non-adaptive and needs ~0.5*n^3 edge-relax operations on a complete graph. We show that every non-adaptive algorithm based on edge-relaxations must do ~0.5*n^3 of these, so Yen's variant is best possible.
Summary: A (strict) saddlepoint of a matrix is an entry that is the (strict) maximum of its row and the (strict) minimum of its column. It was known since 1991 that the strict saddlepoint of an n*n matrix can be found in ~nlogn time, in our SOSA24 paper (below) we showed that it can be found in nlog*(n) time. Here we give a simple, optimal, randomized O(n) time algorithm for this task. It is an interesting open question whether O(n) deterministic runtime is also possible.
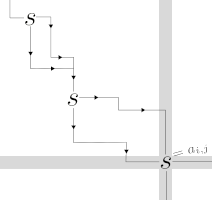
Summary: A (strict) saddlepoint of a matrix is an entry that is the (strict) maximum of its row and the (strict) minimum of its column. It was known since 1991 that the strict saddlepoint of an n*n matrix can be found in ~nlogn time, and it was reasonable to assume this to be tight. Surprisingly, we show that the problem can be solved in nlog*(n) time, where log* is the extremely slowly growing iterated logarithm function. In our ESA 2024 paper (above) we obtain an optimal linear (albeit randomized) algorithm by a different method.
Summary: We show that searches in a binary search tree (BST) with rotations can be served in constant (amortized) time if the search sequence avoids an arbitrary fixed pattern, a question raised in our FOCS 2015 paper, see below. (Whether this can also be achieved by an online algorithm still remains open, up to a tiny gap.) More broadly, we show that pattern-avoidance in the input can make inputs easy for other problems as well. We exemplify this by the k-server and TSP problems.
Follow-up: In FOCS 2024, Opler settles the question of sorting pattern-avoiding sequences in linear time [here]. More examples of algorithmic adaptivity to pattern-avoidance in upcoming work [todo].
Summary: Search trees on trees (STTs) generalize binary search trees (BSTs), but computing (exact or approximate) STTs for a given distribution is much less understood than the BST case. We show that (1) centroid trees (a natural special STT) are a 2-approximation of the optimum, and (2) can be computed in O(nlogn) time (both results hold in a general, weighted case), and (3) various other centroid-related results. Berendsohn's PhD [pdf] and Golinsky's MSc thesis [link] put the results in broader context.
Summary: Suppose we label the edges of a complete bidirected graph with integers. How large can this graph be if none of the cycles has label-sum zero (modulo d). We give improved bounds for this question, also simplifying earlier proofs. We also look at generalizations where the labels are permutations or arbitrary functions [d]->[d]. The more general question has connections with a fair allocation problem.
Follow-up: Similar results and improvements are shown in independent work [here] and [here].
Summary: Search trees on trees (STTs) generalize binary search trees (BSTs): whereas BSTs search over a linear search space, SSTs search over a tree. We show the following: (1) a poly-time algorithm to find an (1+eps)-approximation of the optimal STT for a given search distribution, (2) linear rotation-distance for a broad class of STTs, (3) a generalization of Splay trees to STTs, (4) static optimality of this generalized Splay, asymptotically matching the optimum tree (without knowing the search distribution). Berendsohn's PhD thesis [pdf] puts the results in broader context and has several refinements and extensions.
Summary: We study the smooth heap (introduced in STOC 2018 paper, see below), and a closely related (simpler) heap we call the slim heap, giving a self-contained analysis of both data structures (previously smooth heaps were analyzed in a restricted setting only). We describe and analyse different implementations of operations. The results (for a certain variant) match the best bounds known for self-adjusting heaps. We also test smooth and slim heaps experimentally, observing that they compare favorably with pairing heaps.
Follow-up: In SODA 2023 [ref], Sinnamon and Tarjan prove a related stronger result, showing that the bounds for smooth and slim heaps hold even for the simplest and most natural implementation, matching a known lower bound for self-adjusting heaps. This makes smooth/slim heaps the first (and so far the only known) optimal self-adjusting heaps. See Sinnamon's [thesis] for the full set of results.
Summary: Given m objects (points in d-dimensional space), how many tests (d-dimensional axis-parallel boxes) are needed to identify t defective objects? A test reports whether at least one of the objects in it is defective, and all tests are run in parallel. We introduce this geometric version of the classical group testing problem and give upper and lower bounds for various values of t and d that improve on the trivial bounds.
Summary: Exact exponential-time algorithms are given for the following problems: counting linear extensions when the input poset is two-dimensional, and the jump number problem in arbitrary posets (both running times: ~1.82^n).
Summary: The permutation pattern problem asks whether a given permutation of length n contains a given pattern of length k. We give two new algorithms for the problem: one with running time n^{0.25k+o(k)}, and one with running time O(1.6181^n) or n^{0.5k+o(k)}. The results improve the earlier best bounds for the problem for patterns of size k≈log(n) or larger and reduce the problem to constraint-satisfaction. Our second algorithm uses polynomial space and is simpler than previous approaches for the problem. We include hardness results and improved bounds for special cases, and the counting version of the problem is also studied.
Berendsohn's MSc thesis [pdf] includes refinements of the hardness results with more details. The paper supersedes an earlier report [preprint].
Follow-up: The O(1.618^n) approach is improved to O(1.415^n) through a simple (but clever) modification by Gawrychowski and Rzepecki [here]. Some refined hardness results appear [here].
Summary: Dirac's theorem (1952) is a classical result of graph theory, stating that an n-vertex graph is Hamiltonian if every vertex has degree at least n/2. We show that there are efficient algorithms to determine the Hamiltonicity of a graph, when the degree-requirements of Dirac's theorem are relaxed: we either let the minimum degree be n/2-k, or we let some k vertices have arbitrary degree.
Follow-up: In SODA 2022, Fomin, Golovach, Sagunov, and Simonov [preprint] provide a generalization, confirming the main conjecture of our paper.
Summary: In the many-visits TSP, a salesperson must visit n cities, each of them precisely a prescribed number of times (in the cheapest possible way). We give a polynomial-space algorithm for this problem, with running time that depends single-exponentially on n. This improves on the previous best algorithm by Cosmadakis and Papadimitriou from 1984, that has superexponential time- and space-complexity.
Follow-up: The running time of our algorithms is of the form c^n with c=16 (when polynomial space is used) and c=5 (with exponential space). In ESA 2020, Kowalik, Li, Nadara, Smulewicz, and Wahlström [preprint] improve the first to c≈7.88 and refine the analysis of the second to c=4.
Summary: Using soft heaps, we obtain simpler optimal algorithms for selecting the k-th smallest item from heap-ordered trees, from sets of sorted lists, and from sets of pairwise sums (X + Y), matching, and in some ways extending classical results of Frederickson (1993) and Frederickson and Johnson (1982).
Summary: We improve the analysis of a classical pairing heap variant (Fredman, Sedgewick, Sleator, Tarjan, 1985) and a classical self-adjusting binary search tree heuristic (Sleator, 198x), reducing the gap to the information-theoretic lower bound from roughly (loglog n) to less than (loglog...log n), where log(.) can be iterated any constant number of times.
Follow-up: For multipass pairing heaps further improvements are obtained in SODA 2023 by Sinnamon and Tarjan [link].
Summary: We describe a new connection ("duality") between self-adjusting binary search trees (BSTs) and heaps. This allows us to transfer results between the two settings, obtaining: (1) a broad class of "stable" heap algorithms, (2) instance-specific lower and upper bounds for stable heaps, (3) a new heap data structure called "smooth heap", which we show to be the heap-counterpart of a well-known BST (the "Greedy" BST) that is conjectured to be "instance-optimal", (4) new "offline" BST algorithms.
Follow-up: In further work more general analyses of smooth heaps and their variants have been given (see above), and further intriguing properties of smooth heaps have been found.
Summary: We show that Binary Search Trees (BSTs) with multiple fingers can be efficiently simulated by standard (one-finger) BSTs with rotations. The results connect two prominent online problems: dynamic BSTs and k-server. As an application, we show that BSTs can take advantage of certain regularities in the input, for instance, when accessing items close to some recently accessed item.
Related: The paper builds upon (and partially supersedes) the technical report The landscape of bounds for binary search trees. [pdf]
Some results are found only in the report: a survey of BST properties; new connections/separations between BST properties; a new, more intuitive analysis of Splay trees; a technique for composing ("interleaving") sequences and combining BST properties; an observation about the Move-to-root heuristic.
Summary: We give a new analysis of a classical pairing heap variant (Fredman, Sedgewick, Sleator, Tarjan, 1985), improving the bound on the cost of operations from O(n^0.5) to better than O(n^eps) for any constant eps>0. The main novelty is a potential function that captures rank-differences between nodes.
Summary: We give a polynomial time (1+eps)-approximation for euclidean (and more general) cases of the Traveling-Salesman variant in which no hop may be too short, improving on the earlier best ratio of 2.
Related: Supersedes preliminary paper presented at EuroCG 2016. [pdf]
Summary: The thesis contains results related to binary search trees and the dynamic optimality conjecture, combined from three papers, expanded with a survey of the problem, and some new observations. Also includes a list of 50 concrete open questions, some (a few) of which have been fully or partially solved in the years since.
Summary: Serving a sequence of searches in a binary search tree with rotations is shown to be equivalent with the previously studied problem of finding a sequence of flips between two rectangulations. Connections of both problems to Manhattan networks are also explored.
Related: The core idea of heap/BST duality appears in this paper, developed further in our STOC 2018 smooth heap paper (above). The material also appears (with small updates) as Chapter 5 of my thesis. Note that some simple to state open questions in this paper about flips in rectangulations remain open, and may be not (too) difficult to approach.
Summary: The Hitting Set problem remains hard (in the parameterized sense), even in set systems of very small VC-dimension. If we restrict the structure even more, then Hitting Set is solvable in polynomial time. Our easy class is a generalization of Edge Cover.
Follow-up: The prototype hard problem of Section 2 has been used in several papers to show hardness results in other contexts.
Summary: Searches in binary search trees (BSTs) take almost constant (amortized) time if the search sequence avoids an arbitrary fixed pattern. Moreover, this is attained by Greedy, a general-purpose BST algorithm that is conjectured optimal (for every sequence). Pattern avoiding sequences generalize some well-studied earlier examples, which can be seen as avoiding some particular pattern. Many of the arguments rely on results from forbidden submatrix theory. Part of the material appears (with some updates) as Chapter 4 of my thesis.
Follow-up: Several articles continue the line of work started in this paper, e.g., small refinements of some of the bounds are given [here] or [here]. Our STOC 2024 paper shows the tight, linear bound for BST access with pattern-avoidance (although obtaining the same bound fro Greedy or Splay trees remains open), and extends the idea of adaptivity to pattern avoidance to other algorithmic problems. In FOCS 2024, Opler shows that pattern-avoiding sequences can be sorted in linear time (one of the central questions raised in our work) [here].
Summary: We extend the "geometry of BST" model of Demaine et al. to handle insert and delete operations, and we show that the Greedy algorithm is almost optimal on deque sequences (where insert and delete happens only at the minimum and maximum). The results give circumstantial evidence that Greedy may be instance-optimal. These results can be seen as an instance of the broader phenomenon described in the FOCS 2015 paper (above).
Summary: We give combinatorial conditions that guarantee the efficiency of algorithms for re-arranging binary search trees. This unifies the analysis of several known heuristics, and leads to some new ones that are based on depth-reduction. We also characterize all tree re-arrangement strategies that are local.
Related: The paper supersedes an earlier draft note [pdf] which may nonetheless contain additional intuition. Part of the material appears (with some updates) as Chapter 3 of my thesis.
Summary: We study the problem of partitioning a stream of integers into blocks with roughly equal total value, in one pass. We look at the trade-off between approximation-ratio and amount of memory used.
Summary: We interpret results for set systems, shattering, and VC-dimension, in the context of graph orientations. We thus obtain a number of inequalities (some known, some new) involving distances, flows, connectivity, forbidden subgraphs, etc., in graphs. A warm-up example: the number of orientations of a graph G in which there is an s-to-t directed path equals the number of spanning subgraphs of G in which s and t are connected, for every G, s, t.
Related: The connections in the paper remain somewhat mysterious: it would be interesting to find direct (injective/bijective) proofs for some of the (in)equalities. A follow-up in this direction is [here]. Orientation-results of a similar flavor to some of those in the paper have been shown [here] (on flips) or [here] (on counts). Possible connections to our results or common generalizations would be interesting. This [paper] relates to our results on H-free orientations.
Summary: Given n points in d dimensions, add as few extra points as possible, so that no point can be isolated within a unit box. The problem arises in the context of data privacy. We give approximation and hardness results.
Summary: How to connect n points in the plane with a non-crossing network, so that the average distance between a pair of points is as small as possible. In general, the problem is shown to be hard, in the unit-weight case a non-trivial polynomial-time algorithm is found, and the metric/euclidean case is left open.
Summary: We propose a PCA-like factorization algorithm for binary matrices with missing values, that scales well to very high dimensional and very sparse data. Together with a binarization method, the algorithm directly reconstructs integer entries within a small range, it is thus well-suited for predicting ratings in collaborative filtering.
Misc.
- Useful inequalities cheat sheet, 2012-...
[link to page] [pdf] [ps.gz] - My entry in the Math Genealogy.
To my home page.